ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการตั้งชื่อไม่เหมือนกัน ฟังก์ชันเอกซ์โพเนนเชียลก็เป็นอีกรูปแบบหนึ่งของฟังก์ชันซึ่งเราจะไปดูว่าฟังก์ชันเอกซ์โพนเนน  อ่านเพิ่มเติม

 ฟังก์ชันเชิงเส้น   คือ ฟังก์ชันที่อยู่ในรูป y = ax+b เมื่อ a ,b เป็นจำนวนจริง และ  กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้น ตัวอย่างของฟังก์ชันเชิงเส้น   ได้แก่  อ่านเพิ่มเติม

  ในชีวิตประจำวันจะพบสิ่งที่มีความเกี่ยวข้องกันอยู่เสมอ  เช่น  สินค้ากับราคาสินค้าคนไทยทุกคนจะต้องมีเลขประจำตัวประชาชนเป็นของตนเอง อ่านเพิ่มเติม

      ค่าสัมบูรณ์ของจำนวนจริง a ใดๆ เขียนแทนด้วย |a| หมายถึง ระยะทางจากจุด 0 จนถึงจุด บนเส้นจำนวน ตัวอย่างเช่นเนื่องจากระยะทางต้องมีค่าเป็นจำนวนจริงบวกหรือศูนย์ ดังนั้น บทนิยามของ  อ่านเพิ่มเติม

จำนวนตรรกยะ (rational number) เป็นจำนวนจริงที่สามารถเขียนได้ในรูปเศษส่วนของจำนวนเต็มที่ตัวส่วนไม่เป็นศูนย์ อ่านเพิ่มเติม

เซตของจำนวนจริงประกอบด้วยสับเซตที่สำคัญ  ได้แก่เซตของจำนวนนับ/ เซตของจำนวนเต็มบวก เขียนแทนด้วย  Iอ่านเพิ่มเติม

            

   การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความ  ซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็น อ่านเพิ่มเติม

การให้เหตุผลแบบอุปนัย เป็นวิธีการสรุปผลมาจากการค้นหาความจริงจากการสังเกตหรือการทดลองหลายครั้งจากกรณีย่อยๆ แล้วนำมาสรุปเป็นความรู้แบบทั่วไป อ่านเพิ่มเติม

เป็นการให้เหตุผลโดยอาศัยข้อสังเกตหรือผลการทดลองจากหลาย ๆ ตัวอย่าง มาสรุปเป็นข้อตกลง หรือข้อคาดเดาทั่วไป  หรือคำพยากรณ์ ซึ่งจะเห็นว่าการจะนำเอาข้อสังเกต   หรือผลการท อ่านเพิ่มเติม

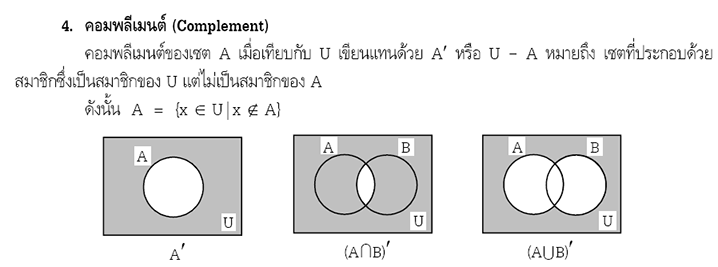
  ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นส่วนหนึ่งของการกระทำระหว่างเซต เรานิยมเขียนออกมาในสองรูปแบบด้วยกันคือแบบสมการ และแผนภาพเวนน์-ออย อ่านเพิ่มเติม

สับเซต บทนิยาม เซต A เป็นสับเซตของเซต B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A  เป็นสมาชิกของเซต B และสามารถเขียนแทนได้ด้วยสัญลักษณ์  อ่านเพิ่มเติม

เอกภพสัมพัทธ์ คือ เซตที่ประกอบด้วยสมาชิกทั้งหมดของสิ่งที่เราต้องการจะศึกษา สามารถเขียนแทนได้ ด้วยสัญลักษณ์   เอกภพสัมพัทธ์ (Relative Universe) ในการพูดถึงเรื่องใดก็ตามใน  อ่านเพิ่มเติม

เซต  เป็นคำที่ใช้บ่งบอกถึงกลุ่มของสิ่งต่างๆ และเมื่อกล่าวถึงกลุ่มใดแน่นอนว่าสิ่งใดอยู่ในกลุ่ม สิ่งใดไม่อยู่ในกลุ่มเซตสระในภาษาอังกฤษ  หมายถึง  กลุ่มของอังกฤษ   อ่านเพิ่มเติม